KL Divergence¶

Module Interface¶

class torchmetrics.KLDivergence(log_prob=False, reduction='mean', **kwargs)[source]

$D_{KL}(P||Q) = \sum_{x\in\mathcal{X}} P(x) \log\frac{P(x)}{Q{x}}$

Where $P$ and $Q$ are probability distributions where $P$ usually represents a distribution over data and $Q$ is often a prior or approximation of $P$ . It should be noted that the KL divergence is a non-symetrical metric i.e. $D_{KL}(P||Q) \neq D_{KL}(Q||P)$ .

As input to forward and update the metric accepts the following input:

p (Tensor): a data distribution with shape (N, d)
q (Tensor): prior or approximate distribution with shape (N, d)

As output of forward and compute the metric returns the following output:

kl_divergence (Tensor): A tensor with the KL divergence

Parameters

log_prob¶ (bool) – bool indicating if input is log-probabilities or probabilities. If given as probabilities, will normalize to make sure the distributes sum to 1.
reduction¶ (Literal[‘mean’, ‘sum’, ‘none’, None]) –
Determines how to reduce over the N/batch dimension:
- 'mean' [default]: Averages score across samples
- 'sum': Sum score across samples
- 'none' or None: Returns score per sample
kwargs¶ (Any) – Additional keyword arguments, see Advanced metric settings for more info.

Raises

TypeError – If log_prob is not an bool.
ValueError – If reduction is not one of 'mean', 'sum', 'none' or None.

Note

Half precision is only support on GPU for this metric

Example

>>> from torch import tensor
>>> from torchmetrics import KLDivergence
>>> p = tensor([[0.36, 0.48, 0.16]])
>>> q = tensor([[1/3, 1/3, 1/3]])
>>> kl_divergence = KLDivergence()
>>> kl_divergence(p, q)
tensor(0.0853)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

plot(val=None, ax=None)[source]

Plot a single or multiple values from the metric.

Parameters

val¶ (Union[Tensor, Sequence[Tensor], None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.
ax¶ (Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis

Return type

Tuple[Figure, Union[Axes, ndarray]]

Returns

Figure and Axes object

Raises

ModuleNotFoundError – If matplotlib is not installed

>>> from torch import randn
>>> # Example plotting a single value
>>> from torchmetrics.regression import KLDivergence
>>> metric = KLDivergence()
>>> metric.update(randn(10,3).softmax(dim=-1), randn(10,3).softmax(dim=-1))
>>> fig_, ax_ = metric.plot()

(Source code, png, hires.png, pdf)

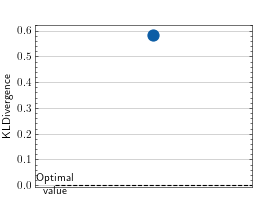
>>> from torch import randn
>>> # Example plotting multiple values
>>> from torchmetrics.regression import KLDivergence
>>> metric = KLDivergence()
>>> values = []
>>> for _ in range(10):
...     values.append(metric(randn(10,3).softmax(dim=-1), randn(10,3).softmax(dim=-1)))
>>> fig, ax = metric.plot(values)

(Source code, png, hires.png, pdf)

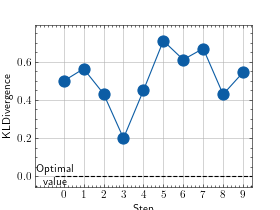
Functional Interface¶

torchmetrics.functional.kl_divergence(p, q, log_prob=False, reduction='mean')[source]

Compute KL divergence.

$D_{KL}(P||Q) = \sum_{x\in\mathcal{X}} P(x) \log\frac{P(x)}{Q{x}}$

Where $P$ and $Q$ are probability distributions where $P$ usually represents a distribution over data and $Q$ is often a prior or approximation of $P$ . It should be noted that the KL divergence is a non-symetrical metric i.e. $D_{KL}(P||Q) \neq D_{KL}(Q||P)$ .

Parameters

p¶ (Tensor) – data distribution with shape [N, d]
q¶ (Tensor) – prior or approximate distribution with shape [N, d]
log_prob¶ (bool) – bool indicating if input is log-probabilities or probabilities. If given as probabilities, will normalize to make sure the distributes sum to 1
reduction¶ (Literal[‘mean’, ‘sum’, ‘none’, None]) –
Determines how to reduce over the N/batch dimension:
- 'mean' [default]: Averages score across samples
- 'sum': Sum score across samples
- 'none' or None: Returns score per sample

Example

>>> from torch import tensor
>>> p = tensor([[0.36, 0.48, 0.16]])
>>> q = tensor([[1/3, 1/3, 1/3]])
>>> kl_divergence(p, q)
tensor(0.0853)

Return type: Tensor