Pearson’s Contingency Coefficient¶
Module Interface¶
- class torchmetrics.PearsonsContingencyCoefficient(num_classes, nan_strategy='replace', nan_replace_value=0.0, **kwargs)[source]
Compute Pearson’s Contingency Coefficient statistic measuring the association between two categorical (nominal) data series.
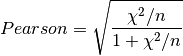
where
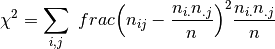
where
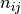 denotes the number of times the values
denotes the number of times the values 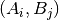 are observed
with
are observed
with 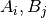 represent frequencies of values in
represent frequencies of values in predsandtarget, respectively.Pearson’s Contingency Coefficient is a symmetric coefficient, i.e.
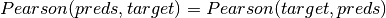 .
.The output values lies in [0, 1] with 1 meaning the perfect association.
- Parameters
num_classes¶ (
int) – Integer specifing the number of classesnan_strategy¶ (
Literal[‘replace’, ‘drop’]) – Indication of whether to replace or dropNaNvaluesnan_replace_value¶ (
Union[int,float,None]) – Value to replaceNaN``s when ``nan_strategy = 'replace'kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
- Returns
Pearson’s Contingency Coefficient statistic
- Raises
ValueError – If nan_strategy is not one of ‘replace’ and ‘drop’
ValueError – If nan_strategy is equal to ‘replace’ and nan_replace_value is not an int or float
Example
>>> from torchmetrics import PearsonsContingencyCoefficient >>> _ = torch.manual_seed(42) >>> preds = torch.randint(0, 4, (100,)) >>> target = torch.round(preds + torch.randn(100)).clamp(0, 4) >>> pearsons_contingency_coefficient = PearsonsContingencyCoefficient(num_classes=5) >>> pearsons_contingency_coefficient(preds, target) tensor(0.6948)
Initializes internal Module state, shared by both nn.Module and ScriptModule.
- update(preds, target)[source]
Update state with predictions and targets.
Functional Interface¶
- torchmetrics.functional.pearsons_contingency_coefficient(preds, target, nan_strategy='replace', nan_replace_value=0.0)[source]
Compute Pearson’s Contingency Coefficient measuring the association between two categorical (nominal) data series.
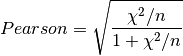
where
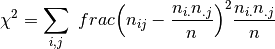
where
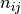 denotes the number of times the values
denotes the number of times the values 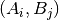 are observed with
are observed with 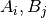 represent frequencies of values in
represent frequencies of values in predsandtarget, respectively.Pearson’s Contingency Coefficient is a symmetric coefficient, i.e.
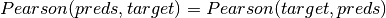 .
.The output values lies in [0, 1] with 1 meaning the perfect association.
- Parameters
1D or 2D tensor of categorical (nominal) data:
1D shape: (batch_size,)
2D shape: (batch_size, num_classes)
1D or 2D tensor of categorical (nominal) data:
1D shape: (batch_size,)
2D shape: (batch_size, num_classes)
nan_strategy¶ (
Literal[‘replace’, ‘drop’]) – Indication of whether to replace or dropNaNvaluesnan_replace_value¶ (
Union[int,float,None]) – Value to replaceNaN``s when ``nan_strategy = 'replace'
- Return type
- Returns
Pearson’s Contingency Coefficient
Example
>>> from torchmetrics.functional import pearsons_contingency_coefficient >>> _ = torch.manual_seed(42) >>> preds = torch.randint(0, 4, (100,)) >>> target = torch.round(preds + torch.randn(100)).clamp(0, 4) >>> pearsons_contingency_coefficient(preds, target) tensor(0.6948)
pearsons_contingency_coefficient_matrix¶
- torchmetrics.functional.nominal.pearsons_contingency_coefficient_matrix(matrix, nan_strategy='replace', nan_replace_value=0.0)[source]
Compute Pearson’s Contingency Coefficient statistic between a set of multiple variables.
This can serve as a convenient tool to compute Pearson’s Contingency Coefficient for analyses of correlation between categorical variables in your dataset.
- Parameters
A tensor of categorical (nominal) data, where:
rows represent a number of data points
columns represent a number of categorical (nominal) features
nan_strategy¶ (
Literal[‘replace’, ‘drop’]) – Indication of whether to replace or dropNaNvaluesnan_replace_value¶ (
Union[int,float,None]) – Value to replaceNaN``s when ``nan_strategy = 'replace'
- Return type
- Returns
Pearson’s Contingency Coefficient statistic for a dataset of categorical variables
Example
>>> from torchmetrics.functional.nominal import pearsons_contingency_coefficient_matrix >>> _ = torch.manual_seed(42) >>> matrix = torch.randint(0, 4, (200, 5)) >>> pearsons_contingency_coefficient_matrix(matrix) tensor([[1.0000, 0.2326, 0.1959, 0.2262, 0.2989], [0.2326, 1.0000, 0.1386, 0.1895, 0.1329], [0.1959, 0.1386, 1.0000, 0.1840, 0.2335], [0.2262, 0.1895, 0.1840, 1.0000, 0.2737], [0.2989, 0.1329, 0.2335, 0.2737, 1.0000]])
