Hinge Loss¶
Module Interface¶
- class torchmetrics.HingeLoss(**kwargs)[source]¶
Compute the mean Hinge loss typically used for Support Vector Machines (SVMs).
This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the
taskargument to either'binary'or'multiclass'. See the documentation ofBinaryHingeLossandMulticlassHingeLossfor the specific details of each argument influence and examples.- Legacy Example:
>>> from torch import tensor >>> target = tensor([0, 1, 1]) >>> preds = tensor([0.5, 0.7, 0.1]) >>> hinge = HingeLoss(task="binary") >>> hinge(preds, target) tensor(0.9000)
>>> target = tensor([0, 1, 2]) >>> preds = tensor([[-1.0, 0.9, 0.2], [0.5, -1.1, 0.8], [2.2, -0.5, 0.3]]) >>> hinge = HingeLoss(task="multiclass", num_classes=3) >>> hinge(preds, target) tensor(1.5551)
>>> target = tensor([0, 1, 2]) >>> preds = tensor([[-1.0, 0.9, 0.2], [0.5, -1.1, 0.8], [2.2, -0.5, 0.3]]) >>> hinge = HingeLoss(task="multiclass", num_classes=3, multiclass_mode="one-vs-all") >>> hinge(preds, target) tensor([1.3743, 1.1945, 1.2359])
BinaryHingeLoss¶
- class torchmetrics.classification.BinaryHingeLoss(squared=False, ignore_index=None, validate_args=True, **kwargs)[source]¶
Compute the mean Hinge loss typically used for Support Vector Machines (SVMs) for binary tasks.
\[\text{Hinge loss} = \max(0, 1 - y \times \hat{y})\]Where \(y \in {-1, 1}\) is the target, and \(\hat{y} \in \mathbb{R}\) is the prediction.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): A float tensor of shape(N, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element.target(Tensor): An int tensor of shape(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain {0,1} values (except if ignore_index is specified). The value 1 always encodes the positive class.
Note
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following output:bhl(Tensor): A tensor containing the hinge loss.
- Parameters:
squared¶ (
bool) – If True, this will compute the squared hinge loss. Otherwise, computes the regular hinge loss.ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
Example
>>> from torchmetrics.classification import BinaryHingeLoss >>> preds = torch.tensor([0.25, 0.25, 0.55, 0.75, 0.75]) >>> target = torch.tensor([0, 0, 1, 1, 1]) >>> bhl = BinaryHingeLoss() >>> bhl(preds, target) tensor(0.6900) >>> bhl = BinaryHingeLoss(squared=True) >>> bhl(preds, target) tensor(0.6905)
- plot(val=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
val¶ (
Union[Tensor,Sequence[Tensor],None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure object and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> # Example plotting a single value >>> from torch import rand, randint >>> from torchmetrics.classification import BinaryHingeLoss >>> metric = BinaryHingeLoss() >>> metric.update(rand(10), randint(2,(10,))) >>> fig_, ax_ = metric.plot()
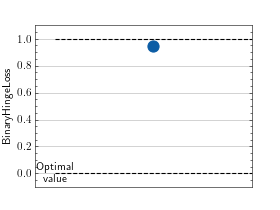
>>> # Example plotting multiple values >>> from torch import rand, randint >>> from torchmetrics.classification import BinaryHingeLoss >>> metric = BinaryHingeLoss() >>> values = [ ] >>> for _ in range(10): ... values.append(metric(rand(10), randint(2,(10,)))) >>> fig_, ax_ = metric.plot(values)
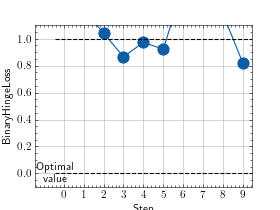
MulticlassHingeLoss¶
- class torchmetrics.classification.MulticlassHingeLoss(num_classes, squared=False, multiclass_mode='crammer-singer', ignore_index=None, validate_args=True, **kwargs)[source]¶
Compute the mean Hinge loss typically used for Support Vector Machines (SVMs) for multiclass tasks.
The metric can be computed in two ways. Either, the definition by Crammer and Singer is used:
\[\text{Hinge loss} = \max\left(0, 1 - \hat{y}_y + \max_{i \ne y} (\hat{y}_i)\right)\]Where \(y \in {0, ..., \mathrm{C}}\) is the target class (where \(\mathrm{C}\) is the number of classes), and \(\hat{y} \in \mathbb{R}^\mathrm{C}\) is the predicted output per class. Alternatively, the metric can also be computed in one-vs-all approach, where each class is valued against all other classes in a binary fashion.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): A float tensor of shape(N, C, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply softmax per sample.target(Tensor): An int tensor of shape(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain values in the [0, n_classes-1] range (except if ignore_index is specified).
Note
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following output:mchl(Tensor): A tensor containing the multi-class hinge loss.
- Parameters:
num_classes¶ (
int) – Integer specifying the number of classessquared¶ (
bool) – If True, this will compute the squared hinge loss. Otherwise, computes the regular hinge loss.multiclass_mode¶ (
Literal['crammer-singer','one-vs-all']) – Determines how to compute the metricignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
Example
>>> from torchmetrics.classification import MulticlassHingeLoss >>> preds = torch.tensor([[0.25, 0.20, 0.55], ... [0.55, 0.05, 0.40], ... [0.10, 0.30, 0.60], ... [0.90, 0.05, 0.05]]) >>> target = torch.tensor([0, 1, 2, 0]) >>> mchl = MulticlassHingeLoss(num_classes=3) >>> mchl(preds, target) tensor(0.9125) >>> mchl = MulticlassHingeLoss(num_classes=3, squared=True) >>> mchl(preds, target) tensor(1.1131) >>> mchl = MulticlassHingeLoss(num_classes=3, multiclass_mode='one-vs-all') >>> mchl(preds, target) tensor([0.8750, 1.1250, 1.1000])
- plot(val=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
val¶ (
Union[Tensor,Sequence[Tensor],None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure object and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> # Example plotting a single value per class >>> from torch import randint, randn >>> from torchmetrics.classification import MulticlassHingeLoss >>> metric = MulticlassHingeLoss(num_classes=3) >>> metric.update(randn(20, 3), randint(3, (20,))) >>> fig_, ax_ = metric.plot()
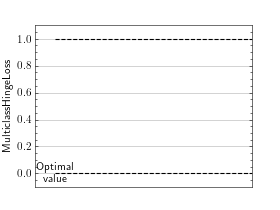
>>> # Example plotting a multiple values per class >>> from torch import randint, randn >>> from torchmetrics.classification import MulticlassHingeLoss >>> metric = MulticlassHingeLoss(num_classes=3) >>> values = [] >>> for _ in range(20): ... values.append(metric(randn(20, 3), randint(3, (20,)))) >>> fig_, ax_ = metric.plot(values)
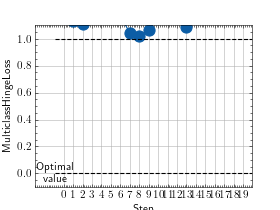
Functional Interface¶
- torchmetrics.functional.hinge_loss(preds, target, task, num_classes=None, squared=False, multiclass_mode='crammer-singer', ignore_index=None, validate_args=True)[source]¶
Compute the mean Hinge loss typically used for Support Vector Machines (SVMs).
This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the
taskargument to either'binary'or'multiclass'. See the documentation ofbinary_hinge_loss()andmulticlass_hinge_loss()for the specific details of each argument influence and examples.- Return type:
- Legacy Example:
>>> from torch import tensor >>> target = tensor([0, 1, 1]) >>> preds = tensor([0.5, 0.7, 0.1]) >>> hinge_loss(preds, target, task="binary") tensor(0.9000)
>>> target = tensor([0, 1, 2]) >>> preds = tensor([[-1.0, 0.9, 0.2], [0.5, -1.1, 0.8], [2.2, -0.5, 0.3]]) >>> hinge_loss(preds, target, task="multiclass", num_classes=3) tensor(1.5551)
>>> target = tensor([0, 1, 2]) >>> preds = tensor([[-1.0, 0.9, 0.2], [0.5, -1.1, 0.8], [2.2, -0.5, 0.3]]) >>> hinge_loss(preds, target, task="multiclass", num_classes=3, multiclass_mode="one-vs-all") tensor([1.3743, 1.1945, 1.2359])
binary_hinge_loss¶
- torchmetrics.functional.classification.binary_hinge_loss(preds, target, squared=False, ignore_index=None, validate_args=False)[source]¶
Compute the mean Hinge loss typically used for Support Vector Machines (SVMs) for binary tasks.
\[\text{Hinge loss} = \max(0, 1 - y \times \hat{y})\]Where \(y \in {-1, 1}\) is the target, and \(\hat{y} \in \mathbb{R}\) is the prediction.
Accepts the following input tensors:
preds(float tensor):(N, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element.target(int tensor):(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain {0,1} values (except if ignore_index is specified). The value 1 always encodes the positive class.
Additional dimension
...will be flattened into the batch dimension.- Parameters:
squared¶ (
bool) – If True, this will compute the squared hinge loss. Otherwise, computes the regular hinge loss.ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.
- Return type:
Example
>>> from torch import tensor >>> from torchmetrics.functional.classification import binary_hinge_loss >>> preds = tensor([0.25, 0.25, 0.55, 0.75, 0.75]) >>> target = tensor([0, 0, 1, 1, 1]) >>> binary_hinge_loss(preds, target) tensor(0.6900) >>> binary_hinge_loss(preds, target, squared=True) tensor(0.6905)
multiclass_hinge_loss¶
- torchmetrics.functional.classification.multiclass_hinge_loss(preds, target, num_classes, squared=False, multiclass_mode='crammer-singer', ignore_index=None, validate_args=False)[source]¶
Compute the mean Hinge loss typically used for Support Vector Machines (SVMs) for multiclass tasks.
The metric can be computed in two ways. Either, the definition by Crammer and Singer is used:
\[\text{Hinge loss} = \max\left(0, 1 - \hat{y}_y + \max_{i \ne y} (\hat{y}_i)\right)\]Where \(y \in {0, ..., \mathrm{C}}\) is the target class (where \(\mathrm{C}\) is the number of classes), and \(\hat{y} \in \mathbb{R}^\mathrm{C}\) is the predicted output per class. Alternatively, the metric can also be computed in one-vs-all approach, where each class is valued against all other classes in a binary fashion.
Accepts the following input tensors:
preds(float tensor):(N, C, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply softmax per sample.target(int tensor):(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain values in the [0, n_classes-1] range (except if ignore_index is specified).
Additional dimension
...will be flattened into the batch dimension.- Parameters:
num_classes¶ (
int) – Integer specifying the number of classessquared¶ (
bool) – If True, this will compute the squared hinge loss. Otherwise, computes the regular hinge loss.multiclass_mode¶ (
Literal['crammer-singer','one-vs-all']) – Determines how to compute the metricignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.
- Return type:
Example
>>> from torch import tensor >>> from torchmetrics.functional.classification import multiclass_hinge_loss >>> preds = tensor([[0.25, 0.20, 0.55], ... [0.55, 0.05, 0.40], ... [0.10, 0.30, 0.60], ... [0.90, 0.05, 0.05]]) >>> target = tensor([0, 1, 2, 0]) >>> multiclass_hinge_loss(preds, target, num_classes=3) tensor(0.9125) >>> multiclass_hinge_loss(preds, target, num_classes=3, squared=True) tensor(1.1131) >>> multiclass_hinge_loss(preds, target, num_classes=3, multiclass_mode='one-vs-all') tensor([0.8750, 1.1250, 1.1000])
