Structure Overview¶
TorchMetrics is a Metrics API created for easy metric development and usage in PyTorch and PyTorch Lightning. It is rigorously tested for all edge cases and includes a growing list of common metric implementations.
The metrics API provides update(), compute(), reset() functions to the user. The metric base class inherits
torch.nn.Module which allows us to call metric(...) directly. The forward() method of the base Metric class
serves the dual purpose of calling update() on its input and simultaneously returning the value of the metric over the
provided input.
These metrics work with DDP in PyTorch and PyTorch Lightning by default. When .compute() is called in
distributed mode, the internal state of each metric is synced and reduced across each process, so that the
logic present in .compute() is applied to state information from all processes.
This metrics API is independent of PyTorch Lightning. Metrics can directly be used in PyTorch as shown in the example:
from torchmetrics.classification import BinaryAccuracy
train_accuracy = BinaryAccuracy()
valid_accuracy = BinaryAccuracy()
for epoch in range(epochs):
for x, y in train_data:
y_hat = model(x)
# training step accuracy
batch_acc = train_accuracy(y_hat, y)
print(f"Accuracy of batch{i} is {batch_acc}")
for x, y in valid_data:
y_hat = model(x)
valid_accuracy.update(y_hat, y)
# total accuracy over all training batches
total_train_accuracy = train_accuracy.compute()
# total accuracy over all validation batches
total_valid_accuracy = valid_accuracy.compute()
print(f"Training acc for epoch {epoch}: {total_train_accuracy}")
print(f"Validation acc for epoch {epoch}: {total_valid_accuracy}")
# Reset metric states after each epoch
train_accuracy.reset()
valid_accuracy.reset()
Note
Metrics contain internal states that keep track of the data seen so far. Do not mix metric states across training, validation and testing. It is highly recommended to re-initialize the metric per mode as shown in the examples above.
Note
Metric states are not added to the models state_dict by default.
To change this, after initializing the metric, the method .persistent(mode) can
be used to enable (mode=True) or disable (mode=False) this behaviour.
Note
Due to specialized logic around metric states, we in general do not recommend
that metrics are initialized inside other metrics (nested metrics), as this can lead
to weird behaviour. Instead consider subclassing a metric or use
torchmetrics.MetricCollection.
Metrics and devices¶
Metrics are simple subclasses of Module and their metric states behave
similar to buffers and parameters of modules. This means that metrics states should
be moved to the same device as the input of the metric:
from torchmetrics.classification import BinaryAccuracy
target = torch.tensor([1, 1, 0, 0], device=torch.device("cuda", 0))
preds = torch.tensor([0, 1, 0, 0], device=torch.device("cuda", 0))
# Metric states are always initialized on cpu, and needs to be moved to
# the correct device
confmat = BinaryAccuracy().to(torch.device("cuda", 0))
out = confmat(preds, target)
print(out.device) # cuda:0
However, when properly defined inside a Module or
LightningModule the metric will
be automatically moved to the same device as the module when using .to(device). Being
properly defined means that the metric is correctly identified as a child module of the
model (check .children() attribute of the model). Therefore, metrics cannot be placed
in native python list and dict, as they will not be correctly identified
as child modules. Instead of list use ModuleList and instead of
dict use ModuleDict. Furthermore, when working with multiple metrics
the native MetricCollection module can also be used to wrap multiple metrics.
from torchmetrics import MetricCollection
from torchmetrics.classification import BinaryAccuracy
class MyModule(torch.nn.Module):
def __init__(self):
...
# valid ways metrics will be identified as child modules
self.metric1 = BinaryAccuracy()
self.metric2 = nn.ModuleList(BinaryAccuracy())
self.metric3 = nn.ModuleDict({'accuracy': BinaryAccuracy()})
self.metric4 = MetricCollection([BinaryAccuracy()]) # torchmetrics built-in collection class
def forward(self, batch):
data, target = batch
preds = self(data)
...
val1 = self.metric1(preds, target)
val2 = self.metric2[0](preds, target)
val3 = self.metric3['accuracy'](preds, target)
val4 = self.metric4(preds, target)
You can always check which device the metric is located on using the .device property.
Metrics and memory management¶
As stated before, metrics have states and those states take up a certain amount of memory depending on the metric. In general metrics can be divided into two categories when we talk about memory management:
Metrics with tensor states: These metrics only have states that are instances of
Tensor. When these kind of metrics are updated the values of those tensors are updated. Importantly the size of the tensors is constant meaning that regardless of how much data is passed to the metric, its memory footprint will not change.Metrics with list states: These metrics have at least one state that is a list, which gets tensors appended as the metric is updated. Importantly the size of the list is therefore not constant and will grow. The growth depends on the particular metric (some metrics only need to store a single value per sample, some much more).
You can always check the current metric state by accessing the .metric_state property, and checking if any of the states are lists.
import torch
from torchmetrics.regression import SpearmanCorrCoef
gen = torch.manual_seed(42)
metric = SpearmanCorrCoef()
metric(torch.rand(2,), torch.rand(2,))
print(metric.metric_state)
metric(torch.rand(2,), torch.rand(2,))
print(metric.metric_state)
{'preds': [tensor([0.8823, 0.9150])], 'target': [tensor([0.3829, 0.9593])]}
{'preds': [tensor([0.8823, 0.9150]), tensor([0.3904, 0.6009])], 'target': [tensor([0.3829, 0.9593]), tensor([0.2566, 0.7936])]}
In general we have a few recommendations for memory management:
When done with a metric, we always recommend calling the reset method. The reason for this being that the python garbage collector can struggle to totally clean the metric states if this is not done. In the worst case, this can lead to a memory leak if multiple instances of the same metric for different purposes are created in the same script.
Better to always try to reuse the same instance of a metric instead of initializing a new one. Calling the reset method returns the metric to its initial state, and can therefore be used to reuse the same instance. However, we still highly recommend to use different instances from training, validation and testing.
If only the results on a batch level are needed e.g no aggregation or alternatively if you have a small dataset that fits into iteration of evaluation, we can recommend using the functional API instead as it does not keep an internal state and memory is therefore freed after each call.
See Advanced metric settings for different advanced settings for controlling the memory footprint of metrics.
Saving and loading metrics¶
Because metrics are essentially just a subclass of torch.nn.Module, saving and loading metrics works in the
same as any other nn.Module, with a key difference. Similar to nn.Module it is also recommended to save the state
dict instead of the actual metric e.g.:
# Instead of this
torch.save(metric, "metric.pt")
# do this
torch.save(metric.state_dict(), "metric.pt")
The key difference is that metric states are not automatically a part of the state dict. This is to make sure that torchmetrics is backward compatible with models that did not use the specific metrics when they were created. This behavior can be overwritten by using the metric.persistent method, which will mark all metric states to also be saved when .state_dict is called. Alternatively, for custom metrics, you can set the persistent argument when initializing the state in the self.add_state method.
Therefore a correct example for saving and loading a metric would be:
import torch
from torchmetrics.classification import MulticlassAccuracy
metric = MulticlassAccuracy(num_classes=5).to("cuda")
metric.persistent(True)
metric.update(torch.randint(5, (100,)).cuda(), torch.randint(5, (100,)).cuda())
torch.save(metric.state_dict(), "metric.pth")
metric2 = MulticlassAccuracy(num_classes=5).to("cpu")
metric2.load_state_dict(torch.load("metric.pth", map_location="cpu"))
# These will match, but be on different devices
print(metric.metric_state)
print(metric2.metric_state)
In the example, we also account for the initial metric state that is being saved on a different device than the metric it is being loaded into by using the map_location argument.
Metrics in Distributed Data Parallel (DDP) mode¶
When using metrics in Distributed Data Parallel (DDP)
mode, one should be aware that DDP will add additional samples to your dataset if the size of your dataset is
not equally divisible by batch_size * num_processors. The added samples will always be replicates of datapoints
already in your dataset. This is done to secure an equal load for all processes. However, this has the consequence
that the calculated metric value will be slightly biased towards those replicated samples, leading to a wrong result.
During training and/or validation this may not be important, however it is highly recommended when evaluating the test dataset to only run on a single gpu or use a join context in conjunction with DDP to prevent this behaviour.
Metrics and 16-bit precision¶
Most metrics in our collection can be used with 16-bit precision (torch.half) tensors. However, we have found
the following limitations:
In general
pytorchhad better support for 16-bit precision much earlier on GPU than CPU. Therefore, we recommend that anyone that want to use metrics with half precision on CPU, upgrade to at least pytorch v1.6 where support for operations such as addition, subtraction, multiplication etc. was added.Some metrics does not work at all in half precision on CPU. We have explicitly stated this in their docstring, but they are also listed below:
You can always check the precision/dtype of the metric by checking the .dtype property.
Metric Arithmetic¶
Metrics support most of python built-in operators for arithmetic, logic and bitwise operations.
For example for a metric that should return the sum of two different metrics, implementing a new metric is an overhead that is not necessary. It can now be done with:
first_metric = MyFirstMetric()
second_metric = MySecondMetric()
new_metric = first_metric + second_metric
new_metric.update(*args, **kwargs) now calls update of first_metric and second_metric. It forwards
all positional arguments but forwards only the keyword arguments that are available in respective metric’s update
declaration. Similarly new_metric.compute() now calls compute of first_metric and second_metric and
adds the results up. It is important to note that all implemented operations always return a new metric object. This means
that the line first_metric == second_metric will not return a bool indicating if first_metric and second_metric
is the same metric, but will return a new metric that checks if the first_metric.compute() == second_metric.compute().
This pattern is implemented for the following operators (with a being metrics and b being metrics, tensors, integer or floats):
Addition (
a + b)Bitwise AND (
a & b)Equality (
a == b)Floordivision (
a // b)Greater Equal (
a >= b)Greater (
a > b)Less Equal (
a <= b)Less (
a < b)Matrix Multiplication (
a @ b)Modulo (
a % b)Multiplication (
a * b)Inequality (
a != b)Bitwise OR (
a | b)Power (
a ** b)Subtraction (
a - b)True Division (
a / b)Bitwise XOR (
a ^ b)Absolute Value (
abs(a))Inversion (
~a)Negative Value (
neg(a))Positive Value (
pos(a))Indexing (
a[0])
Note
Some of these operations are only fully supported from Pytorch v1.4 and onwards, explicitly we found:
add, mul, rmatmul, rsub, rmod
MetricCollection¶
In many cases it is beneficial to evaluate the model output by multiple metrics.
In this case the MetricCollection class may come in handy. It accepts a sequence
of metrics and wraps these into a single callable metric class, with the same
interface as any other metric.
Example:
from torchmetrics import MetricCollection
from torchmetrics.classification import MulticlassAccuracy, MulticlassPrecision, MulticlassRecall
target = torch.tensor([0, 2, 0, 2, 0, 1, 0, 2])
preds = torch.tensor([2, 1, 2, 0, 1, 2, 2, 2])
metric_collection = MetricCollection([
MulticlassAccuracy(num_classes=3, average="micro"),
MulticlassPrecision(num_classes=3, average="macro"),
MulticlassRecall(num_classes=3, average="macro")
])
print(metric_collection(preds, target))
{'MulticlassAccuracy': tensor(0.1250),
'MulticlassPrecision': tensor(0.0667),
'MulticlassRecall': tensor(0.1111)}
Similarly it can also reduce the amount of code required to log multiple metrics
inside your LightningModule. In most cases we just have to replace self.log with self.log_dict.
from torchmetrics import MetricCollection
from torchmetrics.classification import MulticlassAccuracy, MulticlassPrecision, MulticlassRecall
class MyModule(LightningModule):
def __init__(self, num_classes: int):
super().__init__()
metrics = MetricCollection([
MulticlassAccuracy(num_classes), MulticlassPrecision(num_classes), MulticlassRecall(num_classes)
])
self.train_metrics = metrics.clone(prefix='train_')
self.valid_metrics = metrics.clone(prefix='val_')
def training_step(self, batch, batch_idx):
logits = self(x)
# ...
output = self.train_metrics(logits, y)
# use log_dict instead of log
# metrics are logged with keys: train_Accuracy, train_Precision and train_Recall
self.log_dict(output)
def validation_step(self, batch, batch_idx):
logits = self(x)
# ...
self.valid_metrics.update(logits, y)
def on_validation_epoch_end(self):
# use log_dict instead of log
# metrics are logged with keys: val_Accuracy, val_Precision and val_Recall
output = self.valid_metrics.compute()
self.log_dict(output)
# remember to reset metrics at the end of the epoch
self.valid_metrics.reset()
Note
MetricCollection as default assumes that all the metrics in the collection have the same call signature. If this is not the case, input that should be given to different metrics can given as keyword arguments to the collection.
An additional advantage of using the MetricCollection object is that it will
automatically try to reduce the computations needed by finding groups of metrics
that share the same underlying metric state. If such a group of metrics is found
only one of them is actually updated and the updated state will be broadcasted to
the rest of the metrics within the group. In the example above, this will lead to
a 2-3x lower computational cost compared to disabling this feature in the case of
the validation metrics where only update is called (this feature does not work
in combination with forward). However, this speedup comes with a fixed cost upfront,
where the state-groups have to be determined after the first update. In case the groups
are known beforehand, these can also be set manually to avoid this extra cost of the
dynamic search. See the compute_groups argument in the class docs below for more
information on this topic.
- class torchmetrics.MetricCollection(metrics, *additional_metrics, prefix=None, postfix=None, compute_groups=True)[source]¶
MetricCollection class can be used to chain metrics that have the same call pattern into one single class.
- Parameters:
metrics¶ (
Union[Metric,Sequence[Metric],Dict[str,Metric]]) –One of the following
list or tuple (sequence): if metrics are passed in as a list or tuple, will use the metrics class name as key for output dict. Therefore, two metrics of the same class cannot be chained this way.
arguments: similar to passing in as a list, metrics passed in as arguments will use their metric class name as key for the output dict.
dict: if metrics are passed in as a dict, will use each key in the dict as key for output dict. Use this format if you want to chain together multiple of the same metric with different parameters. Note that the keys in the output dict will be sorted alphabetically.
prefix¶ (
Optional[str]) – a string to append in front of the keys of the output dictpostfix¶ (
Optional[str]) – a string to append after the keys of the output dictcompute_groups¶ (
Union[bool,List[List[str]]]) – By default the MetricCollection will try to reduce the computations needed for the metrics in the collection by checking if they belong to the same compute group. All metrics in a compute group share the same metric state and are therefore only different in their compute step e.g. accuracy, precision and recall can all be computed from the true positives/negatives and false positives/negatives. By default, this argument isTruewhich enables this feature. Set this argument to False for disabling this behaviour. Can also be set to a list of lists of metrics for setting the compute groups yourself.
Note
The compute groups feature can significantly speedup the calculation of metrics under the right conditions. First, the feature is only available when calling the
updatemethod and not when callingforwardmethod due to the internal logic offorwardpreventing this. Secondly, since we compute groups share metric states by reference, calling.items(),.values()etc. on the metric collection will break this reference and a copy of states are instead returned in this case (reference will be reestablished on the next call toupdate).Note
Metric collections can be nested at initialization (see last example) but the output of the collection will still be a single flatten dictionary combining the prefix and postfix arguments from the nested collection.
- Raises:
ValueError – If one of the elements of
metricsis not an instance ofpl.metrics.Metric.ValueError – If two elements in
metricshave the samename.ValueError – If
metricsis not alist,tupleor adict.ValueError – If
metricsisdictand additional_metrics are passed in.ValueError – If
prefixis set and it is not a string.ValueError – If
postfixis set and it is not a string.
- Example::
In the most basic case, the metrics can be passed in as a list or tuple. The keys of the output dict will be the same as the class name of the metric:
>>> from torch import tensor >>> from pprint import pprint >>> from torchmetrics import MetricCollection >>> from torchmetrics.regression import MeanSquaredError >>> from torchmetrics.classification import MulticlassAccuracy, MulticlassPrecision, MulticlassRecall >>> target = tensor([0, 2, 0, 2, 0, 1, 0, 2]) >>> preds = tensor([2, 1, 2, 0, 1, 2, 2, 2]) >>> metrics = MetricCollection([MulticlassAccuracy(num_classes=3, average='micro'), ... MulticlassPrecision(num_classes=3, average='macro'), ... MulticlassRecall(num_classes=3, average='macro')]) >>> metrics(preds, target) {'MulticlassAccuracy': tensor(0.1250), 'MulticlassPrecision': tensor(0.0667), 'MulticlassRecall': tensor(0.1111)}
- Example::
Alternatively, metrics can be passed in as arguments. The keys of the output dict will be the same as the class name of the metric:
>>> metrics = MetricCollection(MulticlassAccuracy(num_classes=3, average='micro'), ... MulticlassPrecision(num_classes=3, average='macro'), ... MulticlassRecall(num_classes=3, average='macro')) >>> metrics(preds, target) {'MulticlassAccuracy': tensor(0.1250), 'MulticlassPrecision': tensor(0.0667), 'MulticlassRecall': tensor(0.1111)}
- Example::
If multiple of the same metric class (with different parameters) should be chained together, metrics can be passed in as a dict and the output dict will have the same keys as the input dict:
>>> metrics = MetricCollection({'micro_recall': MulticlassRecall(num_classes=3, average='micro'), ... 'macro_recall': MulticlassRecall(num_classes=3, average='macro')}) >>> same_metric = metrics.clone() >>> pprint(metrics(preds, target)) {'macro_recall': tensor(0.1111), 'micro_recall': tensor(0.1250)} >>> pprint(same_metric(preds, target)) {'macro_recall': tensor(0.1111), 'micro_recall': tensor(0.1250)}
- Example::
Metric collections can also be nested up to a single time. The output of the collection will still be a single dict with the prefix and postfix arguments from the nested collection:
>>> metrics = MetricCollection([ ... MetricCollection([ ... MulticlassAccuracy(num_classes=3, average='macro'), ... MulticlassPrecision(num_classes=3, average='macro') ... ], postfix='_macro'), ... MetricCollection([ ... MulticlassAccuracy(num_classes=3, average='micro'), ... MulticlassPrecision(num_classes=3, average='micro') ... ], postfix='_micro'), ... ], prefix='valmetrics/') >>> pprint(metrics(preds, target)) {'valmetrics/MulticlassAccuracy_macro': tensor(0.1111), 'valmetrics/MulticlassAccuracy_micro': tensor(0.1250), 'valmetrics/MulticlassPrecision_macro': tensor(0.0667), 'valmetrics/MulticlassPrecision_micro': tensor(0.1250)}
- Example::
The compute_groups argument allow you to specify which metrics should share metric state. By default, this will automatically be derived but can also be set manually.
>>> metrics = MetricCollection( ... MulticlassRecall(num_classes=3, average='macro'), ... MulticlassPrecision(num_classes=3, average='macro'), ... MeanSquaredError(), ... compute_groups=[['MulticlassRecall', 'MulticlassPrecision'], ['MeanSquaredError']] ... ) >>> metrics.update(preds, target) >>> pprint(metrics.compute()) {'MeanSquaredError': tensor(2.3750), 'MulticlassPrecision': tensor(0.0667), 'MulticlassRecall': tensor(0.1111)} >>> pprint(metrics.compute_groups) {0: ['MulticlassRecall', 'MulticlassPrecision'], 1: ['MeanSquaredError']}
- add_metrics(metrics, *additional_metrics)[source]¶
Add new metrics to Metric Collection.
- Return type:
- items(keep_base=False, copy_state=True)[source]¶
Return an iterable of the ModuleDict key/value pairs.
- persistent(mode=True)[source]¶
Change if metric states should be saved to its state_dict after initialization.
- Return type:
- plot(val=None, ax=None, together=False)[source]¶
Plot a single or multiple values from the metric.
The plot method has two modes of operation. If argument together is set to False (default), the .plot method of each metric will be called individually and the result will be list of figures. If together is set to True, the values of all metrics will instead be plotted in the same figure.
- Parameters:
val¶ (
Union[Dict,Sequence[Dict],None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.ax¶ (
Union[Axes,Sequence[Axes],None]) – Either a single instance of matplotlib axis object or an sequence of matplotlib axis objects. If provided, will add the plots to the provided axis objects. If not provided, will create a new. If argument together is set to True, a single object is expected. If together is set to False, the number of axis objects needs to be the same length as the number of metrics in the collection.together¶ (
bool) – If True, will plot all metrics in the same axis. If False, will plot each metric in a separate
- Return type:
- Returns:
Either install tuple of Figure and Axes object or an sequence of tuples with Figure and Axes object for each metric in the collection.
- Raises:
ModuleNotFoundError – If matplotlib is not installed
ValueError – If together is not an bool
ValueError – If ax is not an instance of matplotlib axis object or a sequence of matplotlib axis objects
>>> # Example plotting a single value >>> import torch >>> from torchmetrics import MetricCollection >>> from torchmetrics.classification import BinaryAccuracy, BinaryPrecision, BinaryRecall >>> metrics = MetricCollection([BinaryAccuracy(), BinaryPrecision(), BinaryRecall()]) >>> metrics.update(torch.rand(10), torch.randint(2, (10,))) >>> fig_ax_ = metrics.plot()
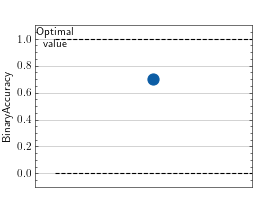
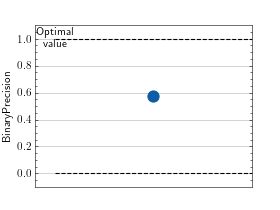
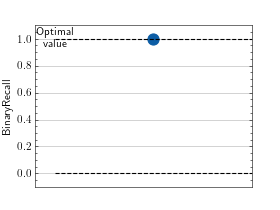
>>> # Example plotting multiple values >>> import torch >>> from torchmetrics import MetricCollection >>> from torchmetrics.classification import BinaryAccuracy, BinaryPrecision, BinaryRecall >>> metrics = MetricCollection([BinaryAccuracy(), BinaryPrecision(), BinaryRecall()]) >>> values = [] >>> for _ in range(10): ... values.append(metrics(torch.rand(10), torch.randint(2, (10,)))) >>> fig_, ax_ = metrics.plot(values, together=True)
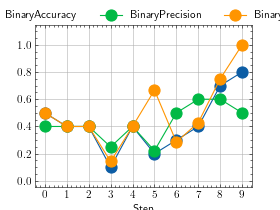
- set_dtype(dst_type)[source]¶
Transfer all metric state to specific dtype. Special version of standard type method.
Metric wrappers¶
In some cases it is beneficial to transform the output of one metric in some way or add additional logic. For this we
have implemented a few Wrapper metrics. Wrapper metrics always take another Metric or (
MetricCollection) as input and wraps it in some way. A good example of this is the
ClasswiseWrapper that allows for easy altering the output of certain classification
metrics to also include label information.
from torchmetrics.classification import MulticlassAccuracy
from torchmetrics.wrappers import ClasswiseWrapper
# creating metrics
base_metric = MulticlassAccuracy(num_classes=3, average=None)
wrapped_metric = ClasswiseWrapper(base_metric, labels=["cat", "dog", "fish"])
# sample prediction and GT
target = torch.tensor([0, 2, 0, 2, 0, 1, 0, 2])
preds = torch.tensor([2, 1, 2, 0, 1, 2, 2, 2])
# showing the metric results
print(base_metric(preds, target)) # this returns a simple tensor without label info
print(wrapped_metric(preds, target)) # this returns a dict with label info
tensor([0.0000, 0.0000, 0.3333])
{'multiclassaccuracy_cat': tensor(0.),
'multiclassaccuracy_dog': tensor(0.),
'multiclassaccuracy_fish': tensor(0.3333)}
Another good example of wrappers is the BootStrapper that allows for easy bootstrapping
of metrics e.g. computation of confidence intervals by resampling of input data.
from torchmetrics.classification import MulticlassAccuracy
from torchmetrics.wrappers import BootStrapper
# creating metrics
wrapped_metric = BootStrapper(MulticlassAccuracy(num_classes=3))
# sample prediction and GT
target = torch.tensor([0, 2, 0, 2, 0, 1, 0, 2])
preds = torch.tensor([2, 1, 2, 0, 1, 2, 2, 2])
# showing the metric results
print(wrapped_metric(preds, target)) # this returns a dict with label info
{'mean': tensor(0.1476), 'std': tensor(0.0613)}
You can see all implemented wrappers under the wrapper section of the API docs.
Module vs Functional Metrics¶
The functional metrics follow the simple paradigm input in, output out. This means they don’t provide any advanced mechanisms for syncing across DDP nodes or aggregation over batches. They simply compute the metric value based on the given inputs.
Also, the integration within other parts of PyTorch Lightning will never be as tight as with the Module-based interface. If you look for just computing the values, the functional metrics are the way to go. However, if you are looking for the best integration and user experience, please consider also using the Module interface.
Metrics and differentiability¶
Metrics support backpropagation, if all computations involved in the metric calculation
are differentiable. All modular metric classes have the property is_differentiable that determines
if a metric is differentiable or not.
However, note that the cached state is detached from the computational graph and cannot be back-propagated. Not doing this would mean storing the computational graph for each update call, which can lead to out-of-memory errors. In practice this means that:
MyMetric.is_differentiable # returns True if metric is differentiable
metric = MyMetric()
val = metric(pred, target) # this value can be back-propagated
val = metric.compute() # this value cannot be back-propagated
A functional metric is differentiable if its corresponding modular metric is differentiable.
Metrics and hyperparameter optimization¶
If you want to directly optimize a metric it needs to support backpropagation (see section above).
However, if you are just interested in using a metric for hyperparameter tuning and are not sure
if the metric should be maximized or minimized, all modular metric classes have the higher_is_better
property that can be used to determine this:
# returns True because accuracy is optimal when it is maximized
torchmetrics.classification.Accuracy.higher_is_better
# returns False because the mean squared error is optimal when it is minimized
torchmetrics.MeanSquaredError.higher_is_better
Advanced metric settings¶
The following is a list of additional arguments that can be given to any metric class (in the **kwargs argument)
that will alter how metric states are stored and synced.
If you are running metrics on GPU and are encountering that you are running out of GPU VRAM then the following argument can help:
compute_on_cpu: will automatically move the metric states to cpu after callingupdate, making sure that GPU memory is not filling up. The consequence will be that thecomputemethod will be called on CPU instead of GPU. Only applies to metric states that are lists.compute_with_cache: This argument indicates if the result after calling thecomputemethod should be cached. By default this isTruemeaning that repeated calls tocompute(with no change to the metric state in between) does not recompute the metric but just returns the cache. By setting it toFalsethe metric will be recomputed every timecomputeis called, but it can also help clean up a bit of memory.
If you are running in a distributed environment, TorchMetrics will automatically take care of the distributed synchronization for you. However, the following three keyword arguments can be given to any metric class for further control over the distributed aggregation:
sync_on_compute: This argument is anboolthat indicates if the metrics should automatically sync between devices whenever thecomputemethod is called. By default this isTrue, but by setting this toFalseyou can manually control when the synchronization happens.dist_sync_on_step: This argument isboolthat indicates if the metric should synchronize between different devices every timeforwardis called. Setting this toTrueis in general not recommended as synchronization is an expensive operation to do after each batch.process_group: By default we synchronize across the world i.e. all processes being computed on. You can provide antorch._C._distributed_c10d.ProcessGroupin this argument to specify exactly what devices should be synchronized over.dist_sync_fn: By default we usetorch.distributed.all_gather()to perform the synchronization between devices. Provide another callable function for this argument to perform custom distributed synchronization.
